Startups rarely stall because founders “lack effort”. They stall because effort is misallocated. Under the crushing weight of runway pressure, you do not need more motivation; you need a decision instrument that tells you exactly what to fix next.
What You'll Learn
- Understand the Entrepreneurial Efficiency Equation (η) as a ratio of internal drivers vs external frictions
Run a 45-minute weekly diagnostic to find the binding variable
Apply a single intervention for 7–14 days (no spread)
See a worked founder scenario that shows η in action
Learn why some startups move faster with fewer resources
The Quantification Gap
Foundational entrepreneurship theories explain the “nature” of the venture. They are intellectually rigorous but practically silent on a Tuesday morning when the burn rate is high and growth is flat.
- Schumpeter (1942): Identifies Creative Destruction but doesn’t map the debris.
- Knight (1921): Distinguishes Uncertainty from Risk but offers no compass.
- Barney (1991): Highlights Resources (RBV) but not the friction of their deployment.
- Sarasvathy (2001): Validates Effectuation but lacks a real-time diagnostic.
Most modern dashboards confuse activity (lines of code, sales calls) with progress (reduction of market uncertainty). We need a model that treats strategy as an engineering problem.
The Entrepreneurial Efficiency Equation (η)
To bridge the gap between theory and weekly execution, we need a way to quantify what’s helping and what’s slowing a venture. The Entrepreneurial Efficiency Equation (η) models progress as a ratio: the internal drivers you can strengthen divided by the external frictions you must reduce or route around. The goal is simple: identify the single binding variable suppressing execution, then intervene with precision.
![]()
Internal Drivers (Numerator)
Variables within your direct control:
𝑃s—Problem-Solving Velocity:
How fast you turn unknowns into decisions (Sarasvathy, 2001).
Proxies: Decision-cycle time, experiment throughput, and time-to-clarity.
𝐼—Innovation / Differentiation
How non-obvious and defensible your advantage is (Amabile, 1996).
Proxies: Measurable differentiation, unique insight, and defensibility.
𝑅—Resources (Fuel + Leverage)
Cash, talent, partner leverage, and distribution access (Baker & Nelson, 2005).
Proxies: Runway, senior talent access, and credibility transfer.
𝐴—Adaptability
How quickly you reconfigure without breaking the system (Eisenhardt & Martin, 2000; Ries, 2011).
Proxies: Pivot speed/quality, feedback loop tightness, and modularity.
External Frictions (Denominator)
Variables that must be systematically reduced or neutralized:
𝑈—Uncertainty (Exponential Drag)
Feasibility risk, demand ambiguity, and regulatory volatility (Knight, 1921).
Proxies: Count of unvalidated critical assumptions and “unknown-unknowns density.”
𝑁—Network Complexity
The “trust tax” of stakeholders and coordination barriers (Hoang & Antoncic, 2003).
Proxies: Number of gatekeepers, approval steps, and coordination paths.
How to use η
A weekly 45-minute diagnostic founders can actually run to prevent “random hustle” and force strategic sequencing.
Step 1—Score the variables (10 minutes)
Use 1–5. The goal is consistency, not “accuracy.” Write exactly one sentence of justification for each score.
Step 2—Identify the binding constraint (10 minutes)
Ask: “Which single variable—if improved by one point—would raise η the most in the next 7–14 days? Look for a dominant limiter:
- If 𝑃s is low: you have a decision/experimentation cadence problem
- If 𝐼 is low: you have a differentiation/architecture problem
- If 𝐴 is low: you have rigidity (process, ego, incentives, architecture)
- If 𝑅 is low: you need leverage or ruthless scope narrowing
- If 𝑈 dominates: you have a feasibility/uncertainty problem
- If 𝑁 dominates: you have a coordination/trust/regulatory problem
Step 3—Choose one intervention (15 minutes)
This is where most teams lose efficiency: they spread effort across everything. Don’t. Pick one binding variable and run a focused intervention for 7–14 days.
If 𝑃s is the bottleneck (Problem-Solving Velocity)
What it looks like: long decision cycles, ambiguous priorities, and slow learning.
Do this next:
- Shorten decision cadence (weekly constraint review + fast commits).
- Increase experiment throughput (smaller tests, faster cycles).
- Maintain a “blocked-by” list of the top 3 unknowns preventing progress.
If 𝐼 is the bottleneck (Innovation / Differentiation)
What it looks like: copycat positioning, incremental features, and a weak “why you” story.
Do this next:
- Force a differentiation answer: why you, why now, and why this approach?
- Reframe constraints until a step-change becomes possible.
- Build an innovation pipeline: insight → hypothesis → prototype.
If 𝑅 is the bottleneck (Resources)
What it looks like: stalled execution due to capacity limits, missing talent, and weak access.
Do this next:
- Substitute leverage for headcount: partnerships, piggyback distribution, and credibility transfer.
- Reduce burn by narrowing scope to constraint-killing work.
- Treat capital as a precision tool, not a blanket.
If 𝐴 is the bottleneck (Adaptability)
What it looks like: slow pivots, defensive decision-making, and brittle product/ops.
Do this next:
- Tighten feedback loops (instrumentation, customer calls, usage data).
- Design modularity so change is not catastrophic.
- Separate identity from idea: pivots are reductions, not defeats.
If 𝑈 dominates (Uncertainty; exponential drag eU)
What it looks like: feasibility isn’t proven; key assumptions are unvalidated; progress is fragile.
Do this next:
- Stage-gate feasibility: prove the hardest thing first.
- Run “killer experiments” designed to disconfirm quickly.
- Delay scaling spend until feasibility stabilizes.
If 𝑁 dominates (Network Complexity)
What it looks like: stakeholder overload, compliance friction, trust barriers, and slow adoption pathways.
Do this next:
- Map stakeholders and cut coordination paths.
- Build trust systems (verification, guarantees, compliance).
- Use anchored partners/institutions to transfer credibility.
Step 4—Re-score and track the slope, not the snapshot
The objective is not a “high η” number—it’s a better trajectory.
- Did the binding variable move meaningfully?
- Did execution become faster, clearer, or less fragile?
- Did you reduce denominator drag or increase numerator force in a measurable way?
If not, your intervention wasn’t targeted enough—or the binding variable was misidentified. Repeat the loop.
Guardrail: Do not “raise R” by default—linear resources can be outpaced by exponential uncertainty eU. If U is dominant, the priority is feasibility-proof through P_s and I, not scaling activity.
A Worked Founder Scenario
Scenario: A founder is building a B2B workflow product for regulated healthcare clinics.
Week 1 scores (1–5):
𝑃s = 2 (slow decisions; experiments take weeks)
𝐼 = 4 (strong product insight)
𝑅 = 3 (some runway, limited team)
𝐴 = 2 (reluctant to revise positioning)
𝑈 = 4 (uncertain adoption + workflow feasibility)
𝑁 = 4 (multiple stakeholders: clinicians, IT, compliance)
Diagnosis: Denominator is crushing execution. But which variable is binding?
The founder realizes: 𝑈 is the true limiter—until feasibility is proven, network complexity work is premature.
Solve for 𝑈:
- Design one “killer experiment”: a 10-day pilot proving integration + workflow compliance in one clinic.
- Stop building features. Stop outbound. Focus on evidence.
The point isn’t the pilot itself—it’s that η forces sequencing: reduce U first so every later action (partnerships, compliance, sales) compounds instead of leaks.
Proof of movement by Friday:
- A signed pilot, integration completed, compliance pathway validated, and a measurable outcome produced.
Week 2 result:
- 𝑈 drops from 4 → 3 (uncertainty reduced with evidence)
- 𝑃s rises 2 → 3 (shorter decision cycles because the constraint is clearer)
Only then does the founder address 𝑁 (coordination drag) with credibility transfer:
- leverage the pilot’s proof to secure an anchored partner or compliance advisor.
Now network complexity starts shrinking because trust is no longer hypothetical.
The utility of η is its ability to stop “random hustle” by forcing you to choose a high-leverage intervention tailored to your specific binding constraint. These playbooks serve as your operational manual once the weekly diagnostic has identified the current limiter.
Diagnostic Archetypes
Once you know the binding variables, most ventures fall into one of three recurring archetypes:
A: Escape Velocity (Deep Tech)
- Constraint: Exponential Drag/Uncertainty
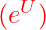
- Strategy: Maximize 𝑃s and 𝐼 to prove feasibility before scaling spend
- Goal: Reduce 𝑈 fast enough that the runway stops evaporating
B: Stamina (Hardware/Bricolage)
- Constraint: Low resources 𝑅
- Strategy: Substitutes capital with high 𝑃s: many low-cost iterations to find the winning architecture 𝐼
- Goal: Reach a prototype that unlocks defensibility and leverage
C: Trust-Moat (Regulated/Platform Markets)
- Constraint: Network Complexity 𝑁
- Strategy: Deploy 𝐴 and 𝑅 specifically to reduce trust and coordination friction
- Goal: Turn the “trust tax” into a moat Competitors cannot cross
Limitations
The Entrepreneurial Efficiency Equation (η) is diagnostic. Its value is constraint clarity and trend direction.
Proxies over precision
Some variables (especially 𝐼 and 𝑈) are subjective. Use consistent proxies and one-sentence justifications to avoid false certainty.
Feedback loops exist
The equation is a snapshot in time. Increasing 𝑅 can reduce 𝐴 through bureaucracy; lowering 𝑈 can change 𝑁 by shifting stakeholder interest. Re-score regularly.
Context matters
Industries weigh variables differently. Deep Tech tends to be 𝑈/𝑃𝑠-dominant; regulated markets skew toward 𝑁; consumer brands often depend more on 𝐼/𝑅. Later versions can introduce coefficients.
Implications for Investors, Policymakers, and Educators
The η equation changes what each stakeholder should optimize for, because execution is a variable system.
For Investors
Evaluate teams by their ability to manage execution variables, not just current traction.
Value Trap: High 𝑅 with low 𝐴 (capital creates rigidity; speed collapses).
Hidden Gem: Low 𝑅 with high 𝑃s and credible innovation 𝐼 (fast learning with real advantage).
Post-investment use: Decide whether your next dollar should fund feasibility reduction (𝑃s/𝐼 to lower 𝑈), adoption pathways (lower 𝑁), or leverage (increase 𝑅 only once 𝐴 can absorb it).
For Policymakers and Ecosystem Builders
If entrepreneurship is weak despite funding, η often points to the real bottleneck.
- Capital fallacy: Abundant 𝑅 does not compensate for high 𝑁 (procurement friction, trust barriers, compliance burden) or volatile 𝑈.
- High-leverage interventions: Reduce 𝑁 through standardized pathways, regulatory clarity, testbeds, and trusted intermediaries, not more grants.
- η in Good policy: lower coordination cost and uncertainty so ventures can compound learning and capability.
For Educators
Most programmes teach planning for 𝑃-like conditions; founders need 𝑁𝑃-like decision heuristics.
- Teach students to identify the binding variable, design constraint-killing experiments, and allocate effort where it changes η.
- Emphasize uncertainty reduction and evidence sequencing over polished plans and linear forecasting.
Conclusion
The Entrepreneurial Efficiency Equation (η) is a definitive decision instrument for the question that matters under runway pressure: What do we fix next?.
It shifts focus from activity to progress by treating execution as a ratio: strengthen internal drivers (𝑃s, 𝐼, 𝑅, 𝐴) while reducing external drag ![]() . Used consistently, η turns venture building from “try harder” into a disciplined practice of constraint identification and removal.
. Used consistently, η turns venture building from “try harder” into a disciplined practice of constraint identification and removal.
In the transition from 𝑁𝑃 complexity to 𝑃 solvability, the winner is not the one who works the hardest, but the one who most accurately identifies and removes the obstacles to work.
References & Further Readings
- Aaronson, S. (2011). Why philosophers should care about computational complexity. Computational Complexity, 20(1), 57–59.
- Amabile, T. M. (1996). Creativity in context. Westview Press.
- Argote, L., & Miron-Spektor, E. (2011). Organizational learning: From experience to knowledge. Organization Science, 22(5), 1123–1137.
- Baker, T., & Nelson, R. E. (2005). Creating something from nothing: Resource construction through entrepreneurial bricolage. Administrative Science Quarterly, 50(3), 329–366.
- Barney, J. (1991). Firm resources and sustained competitive advantage. Journal of Management, 17(1), 99–120.
- Baron, R. A. (2006). Opportunity recognition as pattern recognition: How entrepreneurs “connect the dots” to identify new business opportunities. Academy of Management Perspectives, 20(1), 104–119.
Bontis, N., et al. (2021). Mathematical Modeling of Intellectual Capital and Business Efficiency of Small and Medium Enterprises. Mathematics, 9(18), 2305.
Byers, T. H. (2011). Technology ventures from idea to enterprise.
- Chopra, K. N. (2015). Mathematical Modeling on “Entrepreneurship Outperforming Innovation” for Efficient Performance of the Industry. AIMA Journal of Management & Research, 9(3/4), 1-9.
- Cook, S. A. (1971). The complexity of theorem-proving procedures. Proceedings of the Third Annual ACM Symposium on Theory of Computing (pp. 151–158).
- Eisenhardt, K. M., & Martin, J. A. (2000). Dynamic capabilities: What are they? Strategic Management Journal, 21(10–11), 1105–1121.
Gilbert, N., & Ahrweiler, P. (2013). Agent-based modeling for entrepreneurship research: Opportunities and challenges. Emerald Insight.
Gordijn, J., & Akkermans, H. (2015). Business model analysis using computational modeling: A strategy tool for exploration and decision-making. ResearchGate.
- Indurajani. (2020). Structural equation model of corporate entrepreneurship: A study. SSRN Electronic Journal.
- Karp, R. M. (1972). Reducibility among combinatorial problems. Complexity of Computer Computations (pp. 85–103). Springer.
Kedi, O., Verstiak, A., Kruhlyanko, A., & Ursakii, Y. (2024). Mathematical Modeling for Enhancing Business Strategies in the Hotel and Restaurant Industry. Advances in Nonlinear Variational Inequalities, 28(3s), 386-402.
- Keyhani, M., Lévesque, M., & Madhok, A. (2019). Computational modeling of entrepreneurship grounded in Austrian economics: Insights for strategic entrepreneurship and the opportunity debate. Journal of Business Venturing, 34(5), 105886.
- Knight, F. H. (1921). Risk, uncertainty, and profit. Houghton Mifflin.
- Lee, J. (2013). Mathematical modeling and quantitative analysis of entrepreneurship. Proceedings of the International Conference on Industrial Engineering and Operations Management.
Magd, H., & Thirumalaisamy, R. (2024). Effects of Entrepreneurship, Organization Capability, Strategic Decision Making and Innovation toward the Competitive Advantage of SMEs Enterprises. Research Gate, Retrieved January 24, 2025.
- Mintzberg, H. (1979). The structuring of organizations: A synthesis of the research. Prentice Hall.
- Mitchell, M. (2009). Complexity: A guided tour. Oxford University Press.
- Porter, M. E. (1980). Competitive strategy: Techniques for analyzing industries and competitors. Free Press.
- Ries, E. (2011). The Lean Startup: How constant innovation creates radically successful businesses. Crown Publishing Group.
- Sarasvathy, S. D. (2001). Causation and effectuation: Toward a theoretical shift from economic inevitability to entrepreneurial contingency. Academy of Management Review, 26(2), 243–263.
Sarkar, D., et al. (2024). Analyzing the nexus between entrepreneurship and business mathematics – a comprehensive study on strategic decision-making, financial modeling, and risk assessment in small and medium enterprises (SMEs). International Journal of Research and Review, 11(2), 41-53.
- Schumpeter, J. A. (1942). Capitalism, socialism, and democracy. Harper & Brothers.
- Shane, S., & Venkataraman, S. (2000). The promise of entrepreneurship as a field of research. Academy of Management Review, 25(1), 217–226.
